В своей деятельности человек повсеместно использует модели, то есть создает образ, упрощенную копию того объекта, с которым ему приходится иметь дело.
Модель – это искусственно созданный объект, дающий упрощенное представление о реальном объекте, процессе или явлении, отражающий существенные стороны изучаемого объекта с точки зрения цели моделирования.
Моделирование – это построение моделей, предназначенных для изучения и объектов, процессов или явлений.
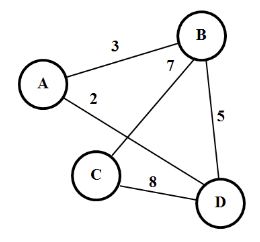
Распространенными информационными моделями являются графики, схемы, таблицы, диаграммы. Одним из распространенных видов моделей являются графы. Граф – это один из способов графического едставления информации. Объекты представлены в нем как вершины (узлы), а связи между объектами как ребра (дуги). Т.е. граф – это набор вершин и связывающих их ребер.
Путь в графе – это конечная последовательность вершин, каждая из которых (кроме последней) соединена со следующей ребром. Граф может содержать циклы (первая вершина пути может совпадать с последней).
Обычно в задачах используют взвешенный граф, т.е. граф, в котором с каждым ребром связано число (вес). Например, расстояние, стоимость и т.д.
Граф может задаваться таблицей, в которой на пересечении строки и столбца с наименованиями вершин записано числовое значение (вес) ребра, соединяющего эти вершины.
Дерево – это граф, не имеющий циклов. В дереве существует один единственный путь между любой парой вершин. Одна из вершин дерева (корень) не имеет входящих ребер, все остальные имеют ровно одно входящее ребро. Вершины, у которых нет исходящих ребер, называются листьями.
1. Поиск графа, соответствующего таблице
Пример 1.
В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице.
Решение:
Сравним значения таблицы и схем:
Согласно таблице вершина A должна быть связана с вершинами B (значение 4) и D (значение 5). Т.е. AB=4, AD=5. На схеме значения указаны около соответствующего ребра. Сразу отбрасываем 1),2),3) схемы, т.к. на них AD не равно 5.
Для уверенности проверим все остальные ребра схемы 4): BC=3, BD=6, что совпадает со значениями таблицы. Правильная схема 4).
Ответ: 4
2. Анализ информации в таблице и графе
Пример 2.
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населенных пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.
Решение:
На графе из вершины В выходит 5 ребер, значит в таблице соответствующий пункт должен иметь дороги в 5 других (строка должна содержать 5 заполненных клеток). Такой пункт в таблице один: П6.
На графе из вершины Е выходит 4 ребра, значит в таблице соответствующий пункт должен иметь дороги в 4 других (строка должна содержать 4 заполненные клетки). Такой пункт в таблице один: П4.
Таким образом, нам нужно найти расстояние между П6 и П4. Согласно таблице оно равно 20.
Ответ: 20
3. Поиск информации в таблице по условию
Пример 3.
Между четырьмя местными аэропортами: ЛУГОВОЕ, ДЯТЛОВО, НИКИТИНО и ОРЕХОВО, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между ними:
Путешественник оказался в аэропорту ЛУГОВОЕ в полночь. Определите самое раннее время, когда он может попасть в аэропорт ОРЕХОВО. Считается, что путешественник успевает совершить пересадку в аэропорту, если между временем прилета в этот аэропорт и временем вылета проходит не менее часа.
1) 12:05 2) 12:50 3)12:55 4) 13:30
Решение:
Можно, конечно, решить эту задачу просто глядя на таблицу и перебирая подходящие варианты, но есть риск ошибиться или пропустить нужную строчку. Поэтому рекомендую нарисовать дерево всех возможных путей из аэропорта ЛУГОВОЕ в ОРЕХОВО:
Средняя ветка не подходит, т.к. между прилетом в аэропорт ДЯТЛОВО (11:15) и вылетом из ДЯТЛОВО в ОРЕХОВО (12:00) интервал меньше часа.
Из оставшихся двух выбираем раннее время прилета: 12:55.
Ответ: 3
4. Выбор таблицы по условию
Пример 4.
В таблицах приведена протяженность автомагистралей между соседними населенными пунктами. Если пересечение строки и столбца пусто, то соответствующие населенные пункты не являются соседними. Укажите номер таблицы, для которой выполняется условие «Максимальная протяженность маршрута от пункта C до пункта B не больше 6». Протяженность маршрута складывается из протяженности автомагистралей между соответствующими соседними населенными пунктами. При этом через любой насеченный пункт маршрут должен проходить не более одного раза.
Решение:
По каждой из схем построим дерево с корнем в точке C и листьями в точке B. При этом нам не нужно строить дерево полностью. Как только найдена ветка с протяженностью больше 6, делаем вывод, что таблица не удовлетворяет указанному условию:
Таблицы 1), 2) и 4) отвергаем уже при анализе первой ветки дерева.
В таблице 3) две ветки вообще не приведут в B, а две другие имеют суммарную длину, не превышающую 6.
Ответ: 3
5. Поиск кратчайшего пути по таблице
Пример 5.
Между населёнными пунктами A, B, C, D, E, F, Z построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и Z (при условии, что передвигаться можно только по построенным дорогам).
1) 13 2) 16 3) 19 4) 21
Решение:
При решении этой задачи тоже не следует полагаться на простой визуальный анализ таблицы. Чтобы избежать ошибок, построим дерево с корнем в вершине A и листьями в вершине Z. При этом нам не нужно выписывать все ветки. Второй путь из A в С (AC=6) длиннее первого (ABC=5), значит и весь маршрут через него будет длиннее.
Второй путь из C в E (CE=10) длиннее первого (CDE=6), значит и весь маршрут через него будет длиннее.
Нам остается сложить длины всех отрезков и выбрать маршрут с наименьшей длиной.
Это верхняя ветка дерева с длиной 16.
Ответ: 2